Kubickou rovnici můžeme vždy zapsat v tomto obecném tvaru:
![]()
Kubická ji nazýváme proto, že obsahuje člen s x3 připomínající objem krychle V = a3. Koeficient a v rovnici musí být nenulový, jinak by se jednalo o kvadratickou rovnici. Kubická rovnice může mít až tři různé kořeny.
Jak řešit kubickou rovnici?
Je to trochu problém, nicméně máme několik možností:
- Převodem na kvadratické a lineární rovnice
- Pomocí kalkulačky
- S podporou počítače
- Přes Cardanův vzorec
- Pomocí některé numerické metody
Převod na kvadratické a lineární rovnice
Nejčastěji využívaná možnost. Provedeme rozklad na součin a dále řešíme rovnice vzniklé z jednotlivých součinitelů. Převádět na součin můžeme pomocí vzorců, vytýkáním a typováním (s následným dělením polynomů).
Příklad 1:

Příklad 2:
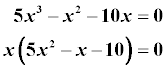
Výpočet kubické rovnice na kalkulačce
Pokud máte pokročilejší hardware typu Casio Algebra FX 2.0, tak vám stačí jít touto cestou:
rovnice (equations) > polynomické (polynomial) > supeň polynomu: 3 > zadání konstant
Buď můžeme použít programy typu Maple, Matlab nebo Excel z balíku MS Office. Pokud nemáte čas si hrát s pokročilými funkcemi Excelu, můžete si vytvořit pouze graf kubické funkce, kde průsečíky s osou x jsou hledané kořeny.
Výpočet pomocí Cardanova vzorce
Cardanův vzorec jsem nikdy nepoužíval, takže na něj pouze odkazuji. Good luck.
Výpočet pomocí některé numerické metody
Tento způsob je asi nejpomalejší a nejpracnější. Pokud bych použili například Newtonovu metodu tečen, museli bychom si nejprve zvolit výchozí interval, a pak vypočítat první iteraci, druhou iteraci, atd., atd...