Soustavy rovnic - řešené příklady

Soustavy rovnic - teorie
Lineární rovnice Kvadratické rovnice Přehled rovnic

Příklad 1: Vypočítejte dosazovací metodou soustavu rovnic o dvou neznámých:

	Z druhé rovnice si vyjádříme x a dosadíme
	ho do první rovnice.
	V první rovnici tak už máme jen jednu neznámou - y.
	Z první rovnice nám vyjde y = 2.
	Výsledek dosadíme do druhé rovnice a dopočítáme x.
	Při počítání samozřejmě není nutné stále opisovat druhou rovnici. Většinou si z ní stačí vyjádřit neznámou, dosadit a pak ji znova použít pro výpočet druhé neznámé.
	Výsledkem je tedy uspořádaná dvojice [1; 2].

 

Příklad 2: Vypočítejte sčítací metodou soustavu rovnic o dvou neznámých:

	Podíváme-li se na obě rovnice, je jasné, že pokud vynásobíme první rovnici -2 a potom ji sečteme druhou rovnicí, tak se nám podaří eliminovat x z druhé rovnice, což je také cílem.
	Z druhé rovnice si potom bez problému vypočteme          y  = -4.
	Vypočtené y dosadíme do první rovnice a dopočítáme x.
	Výsledkem je tedy uspořádaná dvojice [3; -4].

 

Příklad 3: Vypočítejte porovnávací metodou soustavu rovnic o dvou neznámých:

	Porovnávací metoda se s výhodou používá v případech jako je tento - tedy, že jedna strana rovnic je vždy stejná.
y = y	Levé strany si musí být rovny.
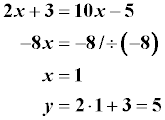	A samozřejmě i pravé strany si musí být rovny. Tím dostaneme lineární rovnici, kterou už můžeme bez větších problémů spočítat. Výsledné x dosadíme do jedné z rovnic v zadání a dopočítáme si y.
	Výsledkem je tedy uspořádaná dvojice [1; 5].

Další řešené příklady soustav lineárních rovnic >>>